Introdução a clusterização e os diferentes métodos

O método de identificação de grupos de dados semelhantes em um conjunto de dados é chamado de cluster. As entidades de cada grupo são comparativamente mais semelhantes às entidades desse grupo do que as dos outros grupos. Neste artigo, estarei conduzindo você pelos tipos de cluster, diferentes algoritmos de clusterização e uma comparação entre dois dos métodos de clusterização mais usados.

Vamos começar.

Visão Geral de clusterização

Clusterização é a tarefa de dividir a população ou os pontos de dados em vários grupos, de modo que os pontos de dados nos mesmos grupos sejam mais semelhantes a outros pontos de dados no mesmo grupo do que os de outros grupos. Em palavras simples, o objetivo é segregar grupos com traços semelhantes e atribuí-los a clusters.

Vamos entender isso com um exemplo. Suponha que você seja o chefe de uma loja de aluguel e queira entender as preferências de seus clientes para expandir seus negócios. É possível que você veja os detalhes de cada cliente e crie uma estratégia comercial única para cada um deles? Definitivamente não. Mas o que você pode fazer é agrupar todos os seus clientes em 10 grupos com base em seus hábitos de compra e usar uma estratégia separada para clientes em cada um desses 10 grupos. E isso é o que chamamos de clustering.

Agora, entendemos o que é clustering. Vamos dar uma olhada nos tipos de clustering.

Tipos de Cluster

De um modo geral,  clusterização pode ser dividido em dois subgrupos:

• Cluster Difícil: No cluster difícil, cada ponto de dados ou pertence a um cluster completamente ou não. Por exemplo, no exemplo acima, cada cliente é colocado em um grupo dos 10 grupos.
• Cluster flexível: No cluster flexível, em vez de colocar cada ponto de dados em um cluster separado, uma probabilidade ou probabilidade de que o ponto de dados esteja nesses clusters é atribuída. Por exemplo, no cenário acima, a cada cliente é atribuída uma probabilidade de estar em qualquer um dos 10 clusters da loja de varejo.

Tipos de algoritmos de clustering

Como a tarefa de agrupamento é subjetiva, os meios que podem ser usados ​​para atingir esse objetivo são muitos. Toda metodologia segue um conjunto diferente de regras para definir a ‘ similaridade’ entre os pontos de dados. De fato, existem mais de 100 algoritmos de clusterização conhecidos. Mas poucos dos algoritmos são usados ​​popularmente, vamos olhá-los detalhadamente:

• Modelos de conectividade: Como o nome sugere, esses modelos baseiam-se na noção de que os dados apontados mais de perto no espaço de dados exibem mais semelhanças entre si do que os pontos de dados mais distantes. Esses modelos podem seguir duas abordagens. Na primeira abordagem, eles começam classificando todos os pontos de dados em clusters separados e, em seguida, agregando-os à medida que a distância diminui. Na segunda abordagem, todos os pontos de dados são classificados como um único cluster e, em seguida, particionados à medida que a distância aumenta. Além disso, a escolha da função de distância é subjetiva. Esses modelos são muito fáceis de interpretar, mas não têm escalabilidade para lidar com grandes conjuntos de dados. Exemplos desses modelos são o algoritmo de clustering hierárquico e suas variantes.

• Modelos centróides: são algoritmos iterativos de clustering nos quais a noção de similaridade é derivada pela proximidade de um ponto de dados ao centróide dos clusters. O algoritmo de clusterização K-Means é um algoritmo popular que se enquadra nessa categoria. Nestes modelos, o não. de clusters necessários no final tem que ser mencionado de antemão, o que torna importante ter conhecimento prévio do conjunto de dados. Esses modelos são executados iterativamente para encontrar o ótimo local.

• Modelos de distribuição:  Esses modelos de armazenamento em cluster são baseados na noção de como é provável que todos os pontos de dados no cluster pertençam à mesma distribuição (por exemplo: Normal, Gaussian). Esses modelos geralmente sofrem de overfitting. Um exemplo popular desses modelos é o algoritmo de maximização de expectativas, que usa distribuições normais multivariadas.

• Modelos de densidade: esses modelos pesquisam o espaço de dados para áreas de densidade variada de pontos de dados no espaço de dados. Ele isola várias regiões de densidade diferentes e atribui os pontos de dados dentro dessas regiões no mesmo cluster. Exemplos populares de modelos de densidade são o DBSCAN e o OPTICS.

Agora vou levá-lo através de dois dos algoritmos de cluster mais populares em detalhes – K Means Clustering e Hierarchical Clustering. Vamos começar.

K-Means Clusters

K means é um algoritmo iterativo de clustering que visa encontrar o máximo local em cada iteração. Este algoritmo funciona nestes 5 passos:

1. Especifique o número desejado de clusters K: Vamos escolher k = 2 para esses 5 pontos de dados no espaço 2-D.

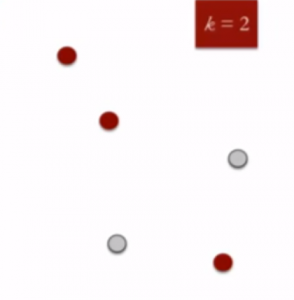
2. Atribuir aleatoriamente cada ponto de dados a um cluster: Vamos atribuir três pontos no cluster 1 mostrados usando a cor vermelha e dois pontos no cluster 2 mostrados usando a cor cinza.

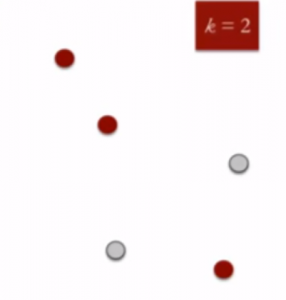
3. Centróides de cluster de cálculo: O centroide dos pontos de dados no cluster vermelho é mostrado usando a cruz vermelha e os do cluster cinza usando a cruz cinza.

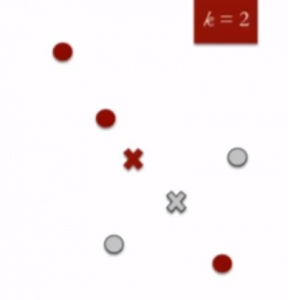
4. Atribua novamente cada ponto ao centróide de cluster mais próximo: Observe que apenas o ponto de dados na parte inferior é atribuído ao cluster vermelho, embora esteja mais próximo do centróide do cluster cinza. Assim, atribuímos esse ponto de dados ao cluster cinza

5. Re-compute centróides de cluster: Agora, re-computando os centróides para ambos os clusters.

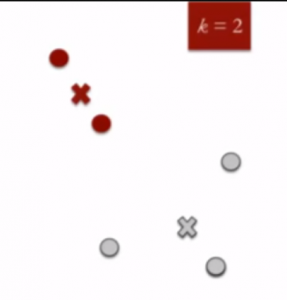
6. Repita os passos 4 e 5 até há melhorias são possíveis: Da mesma forma, vamos repetir os 4 ^th e 5 ^thpassos até que nós vamos chegar optima global. Quando não haverá mais troca de pontos de dados entre dois clusters por duas repetições sucessivas. Ele marcará a terminação do algoritmo se não for explicitamente mencionado.

Clusterização Hierárquica

O clustering hierárquico, como o nome sugere, é um algoritmo que constrói a hierarquia de clusters. Esse algoritmo começa com todos os pontos de dados atribuídos a um cluster próprio. Em seguida, dois clusters mais próximos são mesclados no mesmo cluster. No final, esse algoritmo termina quando há apenas um único cluster.

Os resultados do agrupamento hierárquico podem ser mostrados usando o dendrograma. O dendrograma pode ser interpretado como:

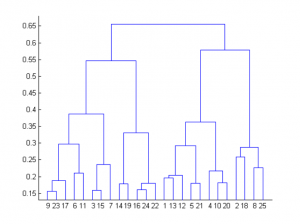
Na parte inferior, começamos com 25 pontos de dados, cada um atribuído a clusters separados. Dois aglomerados mais próximos são então mesclados até que tenhamos apenas um cluster no topo. A altura no dendrograma em que dois clusters são mesclados representa a distância entre dois clusters no espaço de dados.

A decisão do número de clusters que melhor representem diferentes grupos podem ser escolhidos observando-se o dendrograma. A melhor escolha do número de clusters é o número de linhas verticais no dendrograma cortadas por uma linha horizontal que pode atravessar verticalmente a distância máxima sem intersectar um cluster.

No exemplo acima, a melhor escolha de nº de clusters será 4 como a linha horizontal vermelha no dendrograma abaixo abrange distância vertical máxima AB.

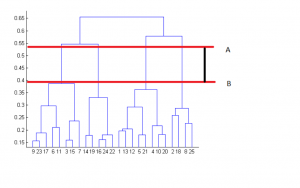
Duas coisas importantes que você deve saber sobre clustering hierárquico são:

• Este algoritmo foi implementado acima usando a abordagem bottom up. Também é possível seguir a abordagem top-down começando com todos os pontos de dados atribuídos no mesmo cluster e realizando divisões recursivamente até que cada ponto de dados seja atribuído a um cluster separado.
• A decisão de fundir dois clusters é tomada com base na proximidade desses clusters. Existem várias métricas para decidir a proximidade de dois clusters:
  • Distância euclidiana: || ab || ₂ = √ (Σ ( ae _– b _i ))
  • Distância Euclidiana Quadrada: || ab || ₂ ² = Σ ((a _i- b _i ) ² )
  • Distância de Manhattan: || ab || ₁ = Σ | a _i- b _i |
  • Distância máxima: || ab || _INFINIDADE = max _i | a _i -b _i |
  • Distância de Mahalanobis: √ ((ab) ^T S ^-1 (-b)) {onde, s: matriz de covariância}

Diferença entre K Means e Hierarchical Clustering

• O armazenamento em cluster hierárquico não pode manipular dados grandes, mas o armazenamento em cluster K Means pode. Isso ocorre porque a complexidade de tempo de K means é linear, ou seja, O (n), enquanto que o de clusterização hierárquica é quadrático, ou seja, O (n ² ).
• Em K Means clustering, uma vez que começamos com a escolha aleatória de clusters, os resultados produzidos pela execução do algoritmo várias vezes podem ser diferentes. Enquanto os resultados são reproduzíveis em clustering hierárquico.
• K means que funciona bem quando a forma dos clusters é hiper esférica (como círculo em 2D, esfera em 3D).
• Clusterização KMeans requer conhecimento prévio de K ou seja, nº. de clusters nos quais você deseja dividir seus dados. Mas, você pode parar em qualquer número de clusters que você achar apropriado em clustering hierárquico, interpretando o dendrograma

Aplicações de Clustering

Clustering tem um grande nº de aplicações espalhadas por vários domínios. Algumas das aplicações mais populares de clustering são:

• Mecanismos de recomendação
• Segmentação de mercado
• Análise de redes sociais
• Agrupamento de resultados de pesquisa
• Imagem Médica
• Segmentação de imagens
• Detecção de anomalia

Notas finais

Neste artigo, discutimos quais são as várias formas de executar o armazenamento em cluster. Ele encontra aplicativos para aprendizado não supervisionado em um grande não. de domínios. Você também viu como pode melhorar a precisão do seu algoritmo de aprendizado de máquina supervisionado usando clustering.

Embora o clustering seja fácil de implementar, você precisa cuidar de alguns aspectos importantes, como tratar os outliers em seus dados e garantir que cada cluster tenha população suficiente. 

Gostou do artigo? De uma olhada em nossos cursos e não fique de fora de aprender mais!